Figure 1. モデル図
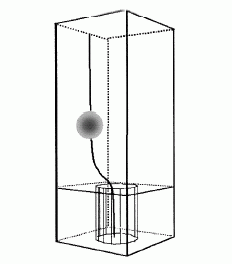
Figure 2.計算結果(粒子阻止率の流束依存性)
まとめ
・Fig.2より、流束が小さい領域と大きい領域で阻止率は増加し、10-4 〜 10-2 m/s の領域においてほぼ一定となっている。この領域では、drag force の方が慣性力より支配的であるため、粒子は流れにのって輸送され膜面に衝突していないと考えられる。また、流束が大きい領域で阻止率が上昇しているのは、速い流れのために粘性力が増加するものの、それ以上に慣性力が大きくなっているためだと考えられる。また、流束が小さい領域での阻止率の増加は、流れが遅いため粒子の運動が自然沈降に近いものになったためだと考えられる。
・実際にNuclepore 膜を用いたPMMA懸濁液の濾過実験では、濾過初期段階の阻止率は流束に依存しないという結果が出ており、その領域もシミュレーションで示された領域と一致した。
・q 値(粒子径と細孔径の比)とこの流束に依存しない領域での阻止率の関係がCFDシミュレーションで再現できることを示せた。
Part2
ナノサイズの細孔をもつ膜における溶媒の透過速度を詳細に解析した。
一般にナノ濾過膜の評価はハーゲン= ポアズイユ則に基づいてなされるが、細孔の大きさがシングルナノに近くなると、流れに対する溶媒分子の大きさが無視できなくなり、連続流体近似が成り立たずハーゲン= ポアズイユ則からのズレが生じると予想される。Fig. 12 に示すような、一定の圧力を溶媒に付加して透過現象をシミュレーションできる特別な分子動力学法(Fluctuating-wallMD)を開発して、膜と溶媒分子との相互作用が透過流束に及ぼす影響を計算した。Fig. 13 は溶媒分子が細孔を透過していく過程のスナップショットであり、はじめ細孔入り口近傍にあった分子が拡散しながら細孔に侵入していく様子が示されている。このようなシミュレーションから、流束のハーゲン= ポアズイユ則からのズレを調べ、細孔内部での溶媒密度の間に一次の相関があることを見出している(Fig. 14)。
Figure 3.モデル図
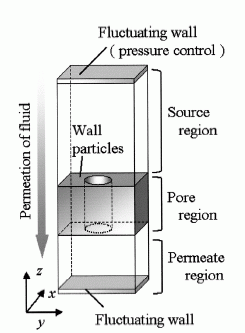
Figure 4.計算結果

Figure 5.計算結果

まとめ
・壁と溶媒分子との相互作用が強いほど、細孔内部での溶媒の密度は溶媒相と比べて大きくなり、透過流束はハーゲン= ポアズイユ則の予想値よりも小さくなる。
液相系膜分離における計算化学の応用展開
|