トップページ＞熱流体事例＞　機能別及び検証事例＞乱流事例＞軸対象回転パイプ内の乱流による輸送

軸対象回転パイプ内の乱流による輸送

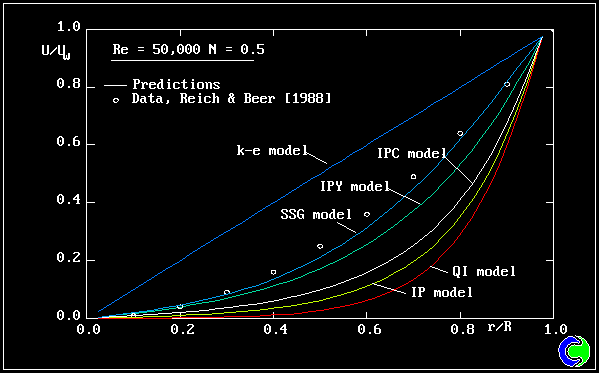
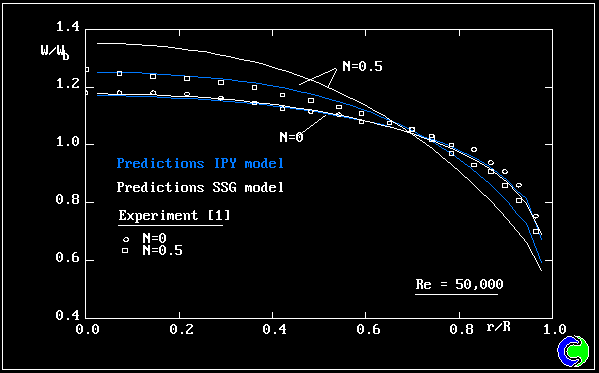
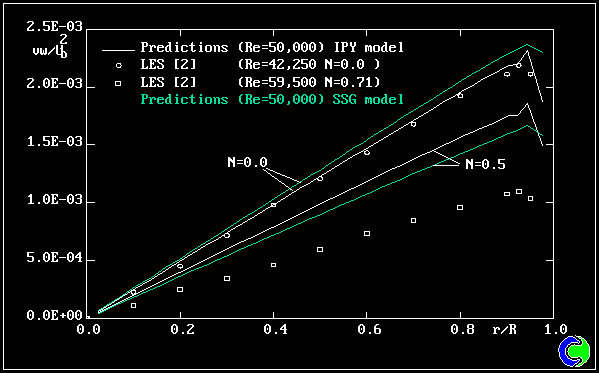
要点：軸対称回転パイプ内における十分発達した流れと熱交換,スワールはパイプ壁面の回転より駆動される,Reynolds 数 Re=5E4 ；Prandtl 数 = 0.71； Swirl数 = 0.5,パイプ壁面から一定の熱流束が供給される,乱流モデル：KE-EP model、RSTM　model（レイノルズ応力モデル）-ipm, ipy, ipc ,qim models（1次のレイノルズ応力モデル）,ssg model（2次のレイノルズ応力モデル）,計算格子：一次元50メッシュ,このシュミレーションはPHOENICSのインプットライブラリー中にあるケースＴ605に該当する

結果：　

	Re=1.E4	Re=2.E4	Re=5.E4
	DATA	RSTM	DATA	RSTM	DATA	RSTM
N = 0	.032	.030	.026	.025	.021	.020
N = 0.5	.026	.025	.022	.020	.017	.016

＊Ｎ：壁速度と軸方向速度の比率

Table 1: Friction factor f　versus Re and N

	Re=1.E4	Re=2.E4	Re=5.E4
	DATA	RSTM	DATA	RSTM	DATA	RSTM
N = 0	30	34	52	56	103	109
N = 0.5	24	27	44	45	87	90

Table 2: Nusselt number　Nu versus Re and N

・RSTMモデルとKE-EPモデルはＮ＝0のときNu数とf数はよく一致する。

・KE-EPモデルでは両方のＮの値でも結果はほぼ同じである。

・結果として、全てのRSTMモデルで Nu数と f数は良く一致している。

fig.1　軸方向速度プロフィル.

fig.2　スワールの速度プロフィル

fig.3　乱流のshear-stressプロファイル

軸対象回転パイプ内の乱流による輸送

PHOENICS　　　CVD　　　2相流　　　事例　　　セミナー　　　サポート　　　受託解析　　　会社概要