By Jalil Ouazzani, ArcoFluid ? Bordeaux, France, Zaim Ouazzani, Arcofluid Consulting LLC,
Orlando, USA ? John Ludwig CHAM Ltd, London, UK.
�͂��߂�
�����ł́A�����肠��Ȃ�3�̈قȂ闬�̂ɂ��O�������V�~�����[�g���邽�߂́A������PHOENICS VOF(Vomume of Fluid) �I�v�V�����̊g���ɂ��ĕ��܂��B��Ƃ��ẮA����������̐�/��/��C�E�ʂ�A�K�X�h�a������̉t�̓S�|/�t�̃X���O/�K�X�E�ʂɌ�����悤�ȁA���x�̈قȂ�t�̂ƋC�̂̑g�ݍ��킹���܂ރV�X�e�����������܂��B3 �̗��̂ւ̊g���ɂ́A��3����\���lj��̃J���[��C3 �̕ۑ������������Ƃ��܂܂�܂��B3�̈قȂ闬�̂��������邽�߂ɁA�������̉^���ʕ������ɂ�����\�ʒ��͂��C�����܂��B
PHOENICS 3�� VOF �̎����́A�C�A�㏸�ɂ��ĂQ�̃P�[�X�Ńe�X�g����܂����B�P�Ԗڂ͒P��t�����ŏ㏸����C�A�̖��A�Q�Ԗڂ�2�̉t�̂��w��ɉt�̂��܂ޓ����ŏ㏸����C�A�̏ꍇ�ł��B�ŏ��̃P�[�X�́AVOF�̊g���ŁA�P����2���V�X�e���ɂ��Č��\����Ă��鐔�l���ʂƈ�v���錋�ʂ������邱�Ƃ������邽�߂ɏd�v�ł��B2�Ԗڂ̃e�X�g�P�[�X�́A���S�ȎO���V�X�e�����V�~�����[�g���āA�e���̕����̕ω��ɉ������C�A�̏㏸��萫�I�ɍČ��ł��邩���������邱�Ƃł��B
���_�I�l�@
C3�̗A���������́A2��VOF�V�~�����[�V�����Ŏg�p���������̃J���[��C1�Ɠ����`���ł��B���̂悤�ɂȂ�܂��B�@
DC3/Dt=0 �@�@�@�@�@�@�@�@(1)�@
PHOENICS�ɂ́A�����I�Ȗ��ɉ����āA(�P)����ۑ��`���������͔�ۑ��`���ʼn����I�v�V����������܂��B�� Cn = 1�Ƃ��邱�Ƃő̐ς̘A�������������A2�̃J���[����A�������܂��B������ Cn ��n���̃J���[���ł��B�����̓� = �� Cn ��n �ɂ���ĕ��ω�����܂��B�� �́A���x�A���S�x�A��M�A�M�`�����A����ё̐ϖc���W���ł��B
PHOENICS��2�� VOF�@�ł́ABrackbill et al (1992) �̕W���I�ȘA���\�ʗ� (CSF)�A�v���[�`���g�p���āA�\�ʒ��͂����̗�fcap = �� ki �� ni�̌`�ʼn^���ʕ������ɓ������܂��B
������ ni = -��Ci/|��Ci| �͊E�ʂ���O�����̖@���x�N�g���ACi��i���̃J���[���A�� = |��Ci| �͊E�ʂ𒆐S�Ƃ���f�B���b�N �f���^���Aki = -(�ށEni) �͊E�ʂ̋ȗ��ł��BCSF �A�v���[�`�̌��_�́A�אڂ��鑊�̖��x���قȂ�ƁA�^���ʕ������ɓ������ꂽ�\�ʒ��͂ɂ��A�E�ʂ̈ʒu�ɑ��ĉ�����̔�Ώ̂ȕ��z�������邱�Ƃł��B���Ƃ��A�����xfcap /�� (�� �̓��[�J�� VOF ���̖��x) �́A���x���Ⴂ�ʑ��ł͂͂邩�ɍ����A���̋t�����l�ł��BCSF �A�v���[�`�ł́A�x�N�g�� fcap�̕����ɉ����āA���Ԃ̊��炩�Ȉڍs�̈悪�����Ȃ���������Ȃ����肵�܂��B���̖��́ABrackbill et al (1992) �ɂ���āA���̂悤�� CSF (DS-CSF) �̖��x�X�P�[�����O���g�p���邱�Ƃɂ��A�V�X�e���ɑ��ĉ�������܂����B
fcap = - �� ki ��Ci ��/<��> (2)�@�@
�����ŁA<��> = (��1 + ��2)/2 �́A�אڂ����P���Ƒ�2���̕��ϖ��x�ł��B����ɂ��A�E�ʂɊւ��đΏ̓I�ȉ����x���z�������܂��B���̌����ł́ATofighi and Yildiz (2013) �ɏ]���āA���ʂƂ��Đ�����\�ʒ��͂�3�̍\���v�f (�e����1��) �ɕ������邱�Ƃɂ��ADS-CSF��3���Ɋg�����܂����B�����̑��ŗL�̗͂͂��ꂼ��A��L�̎� (2) �ɂ���ė^�����܂����A�E�ʕ\�ʒ��͂��g�p�������ɁA3�̑��ɌŗL�̕\�ʒ��͂��g�p����܂��B�����̗͂ɂ̓�n (n = 1,2,3) ���g�p����܂��B��Ő�������悤�ɁA���̃A�v���[�`�͎O���V�X�e���ɂ̂ݗL���ł��B����̈ʑ� n �ɒ��ڂ���ꍇ�A���x�X�P�[�����O�̍l�����́A���� 2 �̈ʑ����A��ԓI�ɖ��x���ω�����P��� n �אڈʑ��Ƃ��Ĉ������Ƃł��B�n�Ɠ��l�ɁADS-CSF �� n�אڑ��̖��x���g�p����ƁA�O���n�̕\�ʒ��͎͂��̂悤�Ɍv�Z�ł��܂��B
fcap = �� fn,cup = - �� ��n kn ��Cn ��/<��>a (3)�@�@
�����ŁAfn,cap �́A<��>n = (��n + ��n_adjacent)/2 �� n�� �� fcap �Ɠ����ł��B
���̒莮���́A�Ώ̓I�ȉ����x�ݏo���悤�ɁA�E�ʑS�̂ɕ\�ʗ͂��ĕ��z���܂��B���ŗL�̕\�ʒ��͂̒l���`���邱�Ƃ͂܂��c���Ă��܂��B���̃A�C�f�A�́A���ʂƂ��Đ�����̓x�N�g���� 3 �̍\���v�f�ł��鑊�ŗL�̗͂ɕ������邱�ƂɊ�Â��Ă��܂� (Tofighi and Yildiz (2013) ���Q��)�B�����̑��ŗL�̗͂́A1 ��ނ̊E�ʂ݂̂��\�� 2 ���V�X�e���̕\�ʗ͂Ɠ������@�Ōʂɏ�������܂��B���̖ړI�̂��߂ɁA�� n �� ���̊Ԃ̊E�ʒ��͂́A�l�H�I�ɓ������ꂽ���ŗL�̕\�ʒ��͂ɂ���ĕ\������A ��n�� = ��n + �Ѓ�
�����ŁA:
��1 = 0.5(��12 + ��13 - ��23)
��2 = 0.5(��12 + ��23 - ��13) (4)
��3 = 0.5(��13 + ��23 - ��12)
�O���V�X�e���̖��_�� 1 �́A���ׂĂ̑������ڐڐG����\�������邱�Ƃł��B�������Ȃ���A�����̏́A�O�q�̕\�ʒ��͂𑊌ŗL�̕\�ʒ��͂̍��v�ɕ������邱�Ƃɂ���Ď����I�ɔ��f����܂��B
�P��t�̒����㏸����C�A�̖��i�n�j
�l������闬��́AHysing et al (2009) �̃e�X�g�P�[�X 2 �Ƃ��Ē�`����Ă���A�t�������㏸����2�����̋C�A�ł��B���̃P�[�X�́A���x�����x�����͂邩�ɒႢ�C�A�Ɋւ�����̂ł��邽�߁A�Y�Ɨp�r���\������̂ł��B��͗̈��} 1 �Ɏ����܂��B�t�� (��1��) �̓����́A��1=1000 kg/m3 ����� ��1=10 Ns/m2 �ƌ��Ȃ���܂��B�K�X (��2��) �̓����́A��2=1 kg/m3 ����� ��2=0.1 Ns/m2 �ɐݒ肳��܂��B�\�ʒ��͂Əd�͉����x�͂��ꂼ�� ��=1.96 N/m �� g=0.98 m/s2 �ɐݒ肳��܂��B
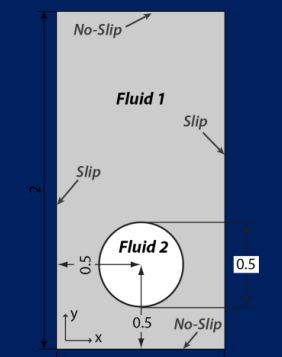
�}�P�@���C�A�̃e�X�g�P�[�X��̓��f���}
���̖��ł́A�C�A�̏d�S�̈ʒu�A�C�A�̏㏸���x�A�C�A�̐^�~�x/���`�x�A�C�A�ʐρA����ѕ\�ʎ��͒���\�����邱�Ƃł��B�����̃p�����[�^�ɂ��� PHOENICS�̌��ʂƁA���ōs�������ʂƔ�r���܂��B�~�`�x�́A���̖ʐϑ����~�̊O����Pa�ɑ���C�A�\�ʂ̊O����Pb�̔�ł��B����͌v�Z�̊J�n���� 1 �̒l�������A�o�u�����ό`����ɂ�Č������܂��B
PHOENICS VOF �V�~�����[�V�����́Ah =1/40�A1/80�A1/160�A�����1/320 �Œ�`�����e���W�����̋ψ�ȃ��b�V�� �T�C�Y h ���g�p���āA�V�~�����[�V�������Ԃ�3 �b�ԂƂ��Ď��s���܂����B��r�̂��߂ɁA�J���[���̗A���������ɂ��������`�Η����̗��U���ɂ��āACICSAM ����� THINC �E�ʉ𑜓x�X�L�[�����g�p���Čv�Z���܂����B
���ʂ�} 2 �` 5 �Ɏ����܂��B�܂��A�} 2 �́A�O���b�h�𑜓x 320 �ł̃o�u���̎��ԕω��̃X�i�b�v�V���b�g�������Ă��܂��B�} 3 �́A���� t = 3 �b�ŃO���b�h�𑜓x 320 �� PHOENICS �œ���ꂽ�C�A�̌`��������Ă��܂��BGamet et al (2018) �� Interfoam �� InterIsoFoam ���g�p���ē������l���ʂ������Ď����܂��B�} 4 �́APHOENICS VOF-CICSAM �œ���ꂽ���ʂł����A���̐}�́A�O���b�h�𑜓x 40�A80�A160�A����� 320 �ł̎��ʒ��S�A�㏸���x�A�^�~�x�������Ă��܂��B�} 5 �́A�𑜓x 320 �ł̏d�S�A�㏸���x�A�^�~�x�ɂ��āAPHOENICS VOF-CICSAM �̌��ʂ� PHOENICS VOF-THINC �œ���ꂽ���ʂ��r�������̂ł��B
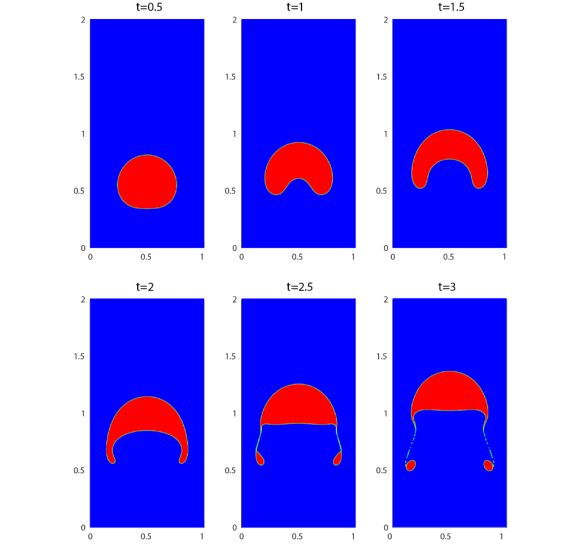
�}�Q�@PHOENICS VOF-THINC �v�Z����
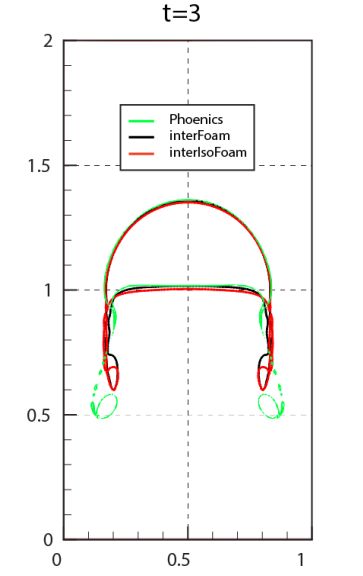
�}�R�@PHOENICS(1/h=1/320),InterFoam(1/h=1/160),InterisoFoam(1/h=160)��t=3s�̋C�A�`��
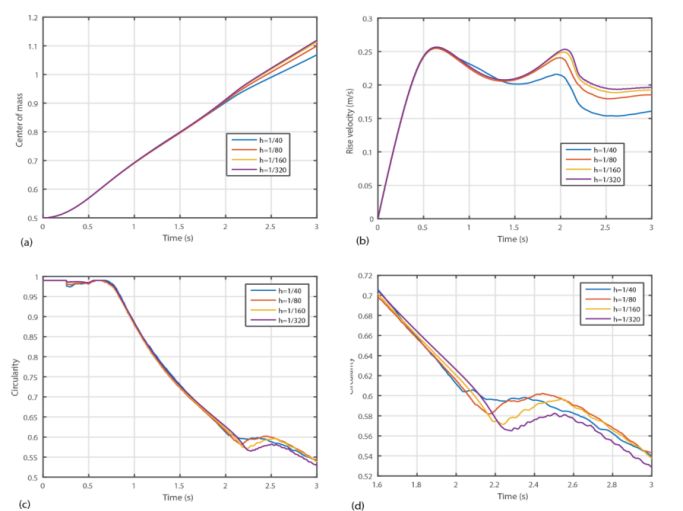
�}�S�@PHOENICS VOF-CICSAM�̎��ԕω��|���b�V���T�C�Y�̔�r�@(a) ���ʒ��S�A(b)�㏸���x�A(c)�^�~�x�A(d)�����C�A�̐^�~�x
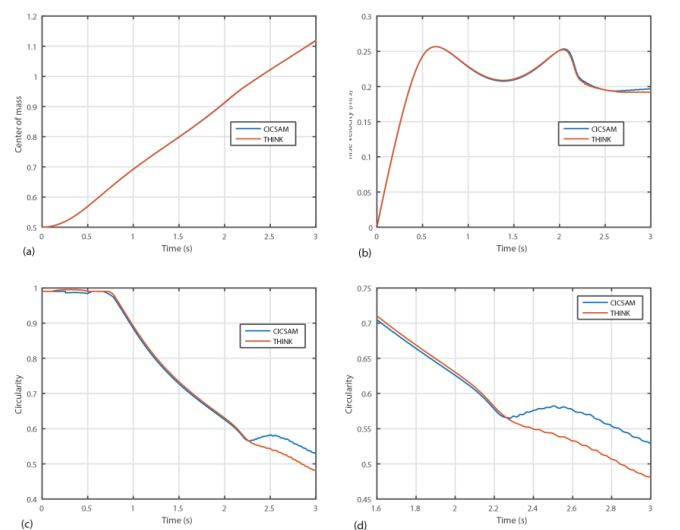
�}�T�@PHOENICS VOF-CICSAM��THINC�̎��ԕω��̔�r�@(a) ���ʒ��S�A(b)�㏸���x�A(c)�^�~�x�A(d)�����C�A�̐^�~�x
VOF �������g�p�ɂ�����CICSAM,THINC�̂ǂ���ł��ǍD�ȓ��삪�����܂����B
����ɁA���̌��ʂ͑��̌��\���ꂽ���ʂƂ悭��r����܂����A���[�������͂܂��c���Ă��܂��B����A�X���[�W���O���x���A�f�B���b�N���̃J�b�g�I�t�A�|���ȂǁAPHOENICS VOF ���\�b�h�̂������̃p�����[�^��ω��������ꍇ�̉e��������\��ł��B
2���t�����̏㏸�C�A�ɂ��3���n�ւ̉��p
���̃Z�N�V�����ł́A �w��ɂȂ��Ă��閧�x�̈قȂ�Q�̉t�̂�ʂ��ď㏸����C�A�ɂ��čl���܂��B�\�ʒ��́A�S�x�A�d�͂��l������܂��B
�v�Z�̈�͐����`�̌`�� �� = [0.0, 1.0] �~ [0.0, 1.0] ���Ƃ�A���ԃ[���ł́A�o�u�� (�t�F�[�Y 1) �� (((?? ?0.5)/??)^2 + ((?? ? 0.325)/??)^2= 1�Œ�`�����ȉ~�`��������܂��B�i�����ƒZ���͂��ꂼ�� a=0.15 �� b=0.075�j��Q���Ƒ�R����y=0.5�̍����ŏ㉺�ɕ������A���x�͂��ꂼ�� 1000 kg/m3 �� 1500 kg/m3 �ł��B�d�͂́A���������̕������� 9.8 m/s2 �̑傫���ō�p���܂��B�v�Z�͂R�p�^�[���s���A�\ 1 �Ɏ����悤�ɁA3�̑��̕������w�肵�Ă��܂��B���b�V�������́A200 �~ 200 �Z�� �ɂ��܂��B

�\�P�@�P�[�X�ԍ��ƕ����l
�@�@�@�@�@�@
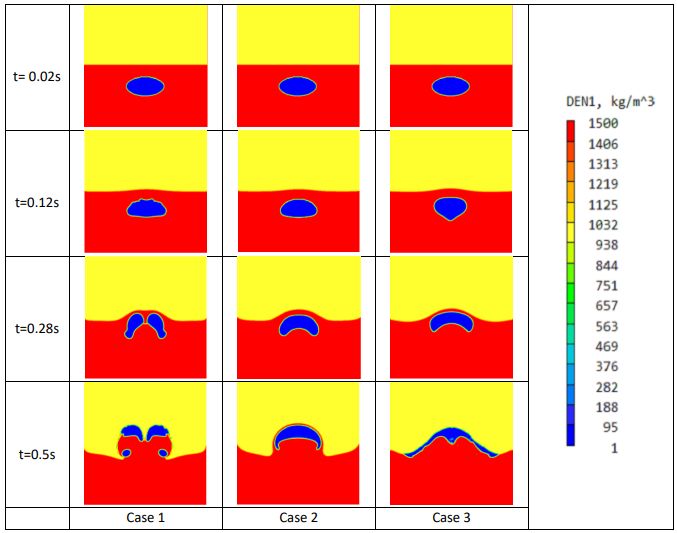
�}�U�@�R�����C�A�㏸���ɂ����閧�x�R���^�[�}
4 �̈قȂ鎞�� (t = 0.02�A0.12�A0.28�A0.5 �b) �ł̐��l���ʂ�} 6 �Ɏ����܂��B
�C�A�͕��͂ɂ���ď㏸���A����Ɉړ�����ɂ�Ă��̌`�����X�������邱�Ƃ��킩��܂��B�C�A�͕��͂ɂ���ď㏸���A��ɍs���قnj`����₷�����Ƃ��킩��܂��B����́A�\�ʗ͂��~�`���ێ��ł���قǑ傫���Ȃ����߂ł��B�S�x�̉e���ɂ��A�C�A�̏㏸���x�Ƃ��̌`�������܂��B
�P�[�X 1�A2�A3 �̃��C�m���Y���́A���ꂼ�� 8267.43�A82.67�A 82.67 �ł��B���C�m���Y�����傫���قǁA�C�A�̘c�݂͑傫���Ȃ�܂��B2 �Ԗڂ̃P�[�X�ł́A���̃P�[�X�����������S�x���g�p���邽�߁A���C�m���Y�����������Ȃ�܂��B�}����P�[�X 2 �ł͋C�A�̘c�݂����Ȃ����Ƃ������Ă��܂��B�P�[�X 1 (����) �ƃP�[�X 3 (�E��) �̌��ʂ��r����ƁA�\�ʒ��͂̉e�����킩��܂��B�P�[�X 3 �̌��ʂ́A�P�[�X 1 �ɔ�ׂĕ\�ʒ��͂��傫���Ȃ������߁A�C�A�����Ȃ����Ƃ��킩��܂��B�P�[�X 3 �̏ꍇ�A�C�A���ŏI�I�Ƀt�F�[�Y 2 �̗��̂Ɋ��S�ɐZ�Ђ���邱�Ƃ������Ă��܂��B
���_
PHOENICS VOF �I�v�V�����́A3 �̈قȂ鍬���肠��Ȃ����̗̂�����V�~�����[�g����悤�Ɋg������܂����B���̎����́A�w��ɕ������ꂽ�t�̓����C�A���㏸������Ō�����܂����B�e���̂̕������p�����[�^�[�ɂ��āA���̕ω��ɉ����ċC�A�̓����Ƙc�݂��萫�I�Ɋm�F�ł��܂����B����̌����́A���\����Ă��鐔�l���ʂƂ̔�r�ɂ��O���V�X�e���̒�ʓI�Ȍ���ړI�Ƃ��Ă��܂��B
|