MMichael Malin、CHAM
はじめに
過去10年、Realisable k-εモデル[1]は、境界層を含む流れが強逆圧力勾配、剥離および再循環流れを伴う場合の適用性が、標準k-εモデルよりも改善された。またRealisable k-εモデルは、円形ジェットの伝播速度の予測性能を大幅に改善すると報告されている。いくつかのPHOENICSユーザーは、剥離と再循環が大きな特徴である建物の周りの流れの数値解析にRealisable k-?モデルを使用している。
Realisable k-εモデルは、2つの点で標準K-?モデルと異なる。Realisable k-εモデルでは、平均二乗渦度変動の輸送方程式対して、異なる輸送方程式により散逸率を表した。このモデルはまた、乱流レイノルズ応力のいくつかの制約に基づいて、異なる渦粘性式を使用した。これは、渦粘性係数Cμが、標準k-εモデルのように定数ではなく、局所的な流れパラメータの関数であることを意味する。
乱流モデル式
Realisable k-εモデルは、以下の式によって定義される。

INFORMによるRealisable k-εモデルの実装
PHOENICSでのこのモデルの実装は、強力なPILおよびINFORM機能を使用することでかなり容易になった。実現方法は、PHOENICSに組み込まれた標準k-ε乱流モデルを起動し、εに対するbuilt-inソースおよびシンク項を無効にして、それらを式(2)に現れるソースおよびシンク項と置き換えることである。置き換え操作はinformコマンドで行う。
INFORM(property ENUT ....)コマンドを使用して、式(5)からの渦粘性を変数Cμで計算する。式(3)、(4)および式(6)〜(8)に現れる様々なモデル係数およびテンソルは、INFORM(stored of ..)コマンドにより計算される。
これらの計算は、乱流周波数EPKE、平均ひずみ速度GEN1、および様々な速度微分関数のSTORE(DUDX、DVDY、...)などを使用。単純化と検証を容易にするため、Cμの関数関係に現れる大部分のパラメータに3D配列が使用されていたので、モデル実装のストレージ要件を削減することができる。
運動量、kおよびεの方程式の壁境界条件は、PLATEおよびBLOCKAGEオブジェクトの利用可能なデフォルト機能によって処理される。
PILとINFORMコーディングを説明するために、乱気流条件を実現するために使用される文を以下に示す。
REAL(C2E);C2E=1.9
(stored of S is GEN1^0.5 with IMAT<100!ZSLSTR)
(stored of ETA is S/EPKE with IMAT<100!ZSLSTR)
(stored of C1E is max(0.43,ETA/(ETA+5.0)) with IMAT<100!ZSLSTR)
(stored of ETRM is (ENUL*EP)^0.5 with IMAT<100!ZSLSTR)
(stored of COEP is :C2E:/(KE+ETRM+1.E-10) with IMAT<100!ZSLSTR)
(Stored of VAEP is C1E*S/COEP with IMAT<100!ZSLSTR)
* Deactivate standard EP source term
COVAL(KESOURCE,EP,ZERO,ZERO)
* Realisable EP source terms
INTEGER(EPLIN);EPLIN=1
IF(EPLIN.EQ.0) THEN
** simple linearisation
(source of EP at KESOURCE is COVAL(COEP*EP,VAEP))
ELSE
** alternative linearisation
(source of EP at KESOURCE is COVAL(FIXFLU,C1E*S*EP))
PATCH(KES2,PHASEM,1,NX,1,NY,1,NZ,1,LSTEP)
(source of EP at KES2 is COVAL(4.*COEP*EP/3.,0.25*EP))
ENDIF
検証
Realisable k-εモデルについて、チャネルとパイプの流れ、バックステップ流れ、平面および円形ジェット、内表面の四角リブを取り付けた2次元チャネル流れ、内表面にキューブを取り付けた3次元チャネル流れを用いて検証した。Realisable k-εモデルは、標準k-εモデルと比べて、計算時間が35%増える。
Realisable k-εモデルは、kおよびε方程式に対して、運動量方程式と同じ大きさ緩和係数で容易に収束する。例外は平面および円形のジェットである。この2種類のケースでは、均一な放出速度を仮定することで発生する大きな速度勾配によって収束が困難になる。これらの問題は、乱流動粘度vtに20%の線形緩和を使用し、vtの上限を設定することで収束過程で生じる非物理的値を避けることによって容易に解決できる。
バックステップ流れ:最初のケースは、1.5の拡張比を有するチャネルにおける2次元バックステップ流れである。レイノルズ数45,000は、ステップ高さHに基づいて定義する。入口および出口面は4Hおよび20H下流にそれぞれ位置に設置する。
数値計算には、垂直50×縦60のメッシュを使用した。図1は、Realisable k-εモデルによって計算した速度ベクトルを示す。ステップのエッジは、ステップ下流の再循環領域の形成および流れの分離点を固定を促進することがわかる。
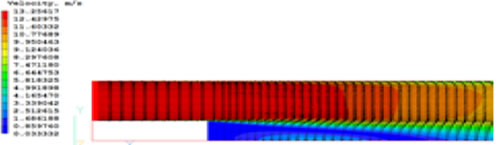
Fig 1: Backward Facing Step: Velocity vectors and separation zone.
表1では、ステップ後方の再付着長さを比較している。標準k-εモデルは、再付着長さを約18%過小評価している。RNGとChen Kimモデルはデータの7%以内で一致するに対して、Realisable k-εモデルは優れた値が得られ、実験結果と良好な一致が確認できた。

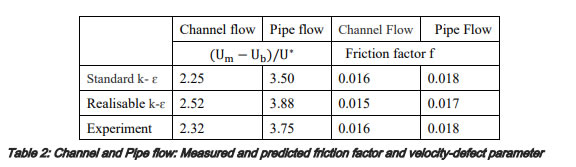
両モデルとも実験結果と良好に一致してすることがわかる。Realisable k-εモデルによって生成される速度欠陥パラメータが標準k-εより大きいのは、方程式(6)から求まるCμが大きめに計算されることに関係する。
平面および円形ジェット:表3では、停滞した空間に入ってくる平面と円形ジェットの伝播速度について比較した。

この表は、標準k-εモデルとRealisable k-εモデルの両方が、平面ジェットの正しい拡散率を正しく計算しているものの、標準k-εモデルは円形ジェットの伝播速度を過大評価する。Realisable k-εモデルが追加されたことにより、この問題が解決された。
内面に四角リブが付くチャネル流れ:ここでは、内面に四角いリブが取り付けられたチャネルを定常の2次元乱流が流れる場合について調べた。リブの高さHは流路の高さの8.5%であり、流路のバルク速度およびリブの高さHに基づくレイノルズ数は300,000である。入口はリブの6H上流に位置し、出口は20Hリブの下流に位置する。計算格子は縦36×横80のメッシュを使用した。
ここでは、流れの分離を特徴付ける主なパラメータは、リブの後方の分離域長さLsである。いくつかの乱流モデルの実験結果と計算結果を表4に示す。

この事例では、Realisable k-εモデルは、Lsを過小評価する標準k-εモデルより優れた結果を得ている。Realisable k-εモデルはRNGモデルと同様に機能するが、最良結果はリブ正面の停滞領域での乱れ発生問題を解決するために開発されたPHOENICSのKato-Launder k-εモデルで得られている。
内面にキューブを取り付けたチャネル流れ:最後に、内面にキューブ取り付けたチャネルを流れる3次元乱流について比較検討する。キューブはチャネル高さの50%を占める。チャネルのバルク速度および立方体の高さHに基づくレイノルズ数は40,000である。入口は立方体の7H上流に位置し、出口10Hは立方体の下流に位置する。
対称性を利用し、流れ幅の半分だけ計算する。40×40×88のメッシュが計算に用いられた。解析領域の幅は4.5Hである。
主渦が立方体周りの馬蹄渦として後流に包まれることが知られているが、ここでは簡単のため流れが立方体の前で分離して1次および2次渦を形成し、定常流れになると推定する。流れは、立方体の正面のコーナーで上面と側壁に分かれる。その後、上面ではなく、側壁に再付着する。
馬蹄渦と相互作用する立方体の後ろに大きな剥離領域が発生する。実験では、側壁から渦放出が観察され、後流との運動量交換のため、定常計算で報告されたものより短い分離距離につながる。
この場合、分離を特徴付ける主なパラメータは、正面のよどみ点Ys/H、一次流れ分離点Lf/H、上面再付着点Lr/Hおよび立方体後ろの分離域の長さLb/Hである。図2は、チャネル中央部における計算速度ベクトルを示す。立方体の前後の再循環領域は明白である。
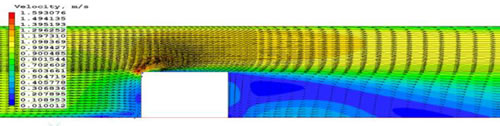
Figure 2: Surface-mounted Cube: Velocity vectors and separation zones fore and aft of the cube at the channel mid section.
表5では、いくつかの乱流モデルのLb/Hの実験結果と計算結果を比較した。

Table 5: Surface-mounted cube: Measured and predicted separation lengths behind the cube.
表5に示す結果は、格子に依存するもの、メッシュ数は上面の予想される剥離を再現するためには不足するし、上流側の分離領域を適切に捉えには足りない。すべてのモデルはLbが大きく計算され、標準k- εモデルは最も実験結果に近い。ほかのモデルは、剥離域においてより低い渦粘性を予測する傾向があるため、標準k- εモデルよりも長い分離領域を形成する。
現在の計算ではメッシュ分解能が不十分であるが、分離長さの計算精度を大幅に向上させるには非定常効果を含める必要があると思われる。重要な近壁領域で非常に細かいメッシュを使用するには、本シミュレーションで使用された高レイノルズ数壁関数を無効にする可能性が高いため、慎重に検討する必要がある。
結論
Realisable k-εモデルを、INFORMおよびPILコマンドを使用してQ1ファイルを修正することで、PHOENICSコードに実装した。乱流モデルの実装は、良好な収束性と合理的な結果を得た多数のケースから検証されている。Realisable k-εモデルは、バックステップ流れ、乱流ジェット、四角いリブ付きチャネル流れで標準k-εモデルおよびそのバリエーションより良好な結果を出している。他の場合では、Realisable k-εモデルはChen-KimおよびRNGバリエーションより経済的である。基本的なモデルテストが完了したので、いくつかの補助変数のWhole Filedストレージを削除することによって、現在の実装を改良できる。このモデルは、3D産業および風工学のにも使用できるだろう。
参考文献
1.Shih,T.-H., Liou,W.W., Shabbir,A., Yang,Z. & Zhu. J, "A New ke Eddy-Viscosity Model for High Reynolds Number Turbulent Flows - Model Development and Validation. Computers Fluids, 24(3):227-238, (1995).
|