流体解析において、乱流は以下の性質をもつ流体運動の一つです。
・空間的及び時間的には非常に不安定、不規則
・3次元的現象(たとえ解析する流れが2次元的であっても)
・常にrotational な性質をもち、高レイノルズ数
・散逸性をもつ(エネルギーが粘性応力により熱に変換される)
・強い拡散性をもつ(混合が速い)
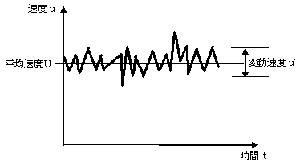
乱流変動は、分子拡散よりも運動量の移動から生成されます。また、乱流の振る舞いは広い周波数帯をもち、ある体積内では大きい渦と小さい渦が重なりあい存在します。
大きい渦は、低周波の変動で流れ場と同程度の規模で、運動量輸送の大部分を占めます。小さい渦は、高周波の
変動で粘性力によって決定されます。
・乱流モデル ⇒ 拡散の増加 ⇒ 渦粘性係数
または、
・乱流モデル ⇒ 拡散の増加 ⇒ 拡散ソース
境界条件に注意し、安定した計算手法を用いれば、乱流であってもこれらの式から計算することができます。このように
直接計算する方法は直接シミュレーション(DNS)と呼ばれますが、実際にはあまり用いられません。
その理由は、エネルギ散逸の作用に相当する小さいスケールから大きいスケールまでの全ての渦を表現するだけの大規模な
計算格子が必要であることがあげられます。また、非常に速い変動を解くため、シミュレーションで使用する時間ステップを
十分に小さくしなければならないこともDNS が用いられない理由の一つです。
実際の工学的に要求される流れのレイノルズ数では、DNS計算を現在の計算機で行うことは不可能です。
そこで、乱流計算するために、ラージエディーシミュレーション(LES)と乱流モデリングという、異なる2つの考え方があります。
【LES の概念】
◎3次元、時間依存性があるナビエ・ストークス方程式を解きます。
◎large-scale motion の直接シミュレーション
◎解析グリッドスケールより小さい乱流現象についてはsub-grid-scale (SGS)モデルを
使用します。
LES の長所は、通常モデル化が困難な大きい渦に対して直接シミュレーションできる点です。
短所としては、次のようなものが挙げられます。
◎高レイノルズ数の流れでは、計算量が非常に多くなります。
◎初期条件及び境界条件の設定が困難です。
◎流れが2 次元的であっても、乱流現象を正
【乱流モデルの分類】
◎0 方程式モデル
Vs とLs は局所的な平均流速の値から計算されます。
(たとえば、プラントルの混合長モデル)
◎1 方程式モデル
Vs は適切な輸送方程式(通常は乱流エネルギーKE)から計算されます。
長さスケールLs は経験値から仮定します。(たとえば、プラントルのKE-L モデル)
◎2 方程式モデル
Vs とLs は、通常KE と散逸率EP の輸送方程式から両方とも計算されます。
◎レイノルズ応力/ 流束輸送モデル
レイノルズ応力と流束の輸送方程式及び長さスケールの輸送方程式(通常は散逸速度EP)を
解きます。
◎代数応力/ 流束モデル
応力/ 流束輸送方程式を、簡略化した代数式で置き換え、乱流の未知数を求めます。
◎LES モデル
【LES の概念】参照
|
